Spin-polarization
This guide aims to give a general overview of spin-polarized (sp)GFNn-xTB calculations within the xtb program package.
Note
This feature is available in xtb in version 6.6.1 and upward via the tblite.
General description
GFN1-xTB and GFN2-xTB both treat open-shell systems in an restricted open-shell fashion since their energy expressions are spin-independent. Therefore, higher electron spin multiplicities will always be higher in energy than the low-spin multiplicities. However, the methods are occupation dependent and the geometries of high-spin states can still be optimized.
spGFNn-xTB
To remedy this issue the spin-polarized GFN1 and GFN2-xTB methods (spGFNn-xTB) have been developed and are available in xtb via the tblite library with the call:
> xtb <geometry_file> --spinpol --tblite
Note
The spin polarization will only affect the energies of open-shell configurations and not of singlets
Example
As example we will calculate the spin splittings of a mixed-valence FeCo complex with spGFN2-xTB to find the electronic ground state:
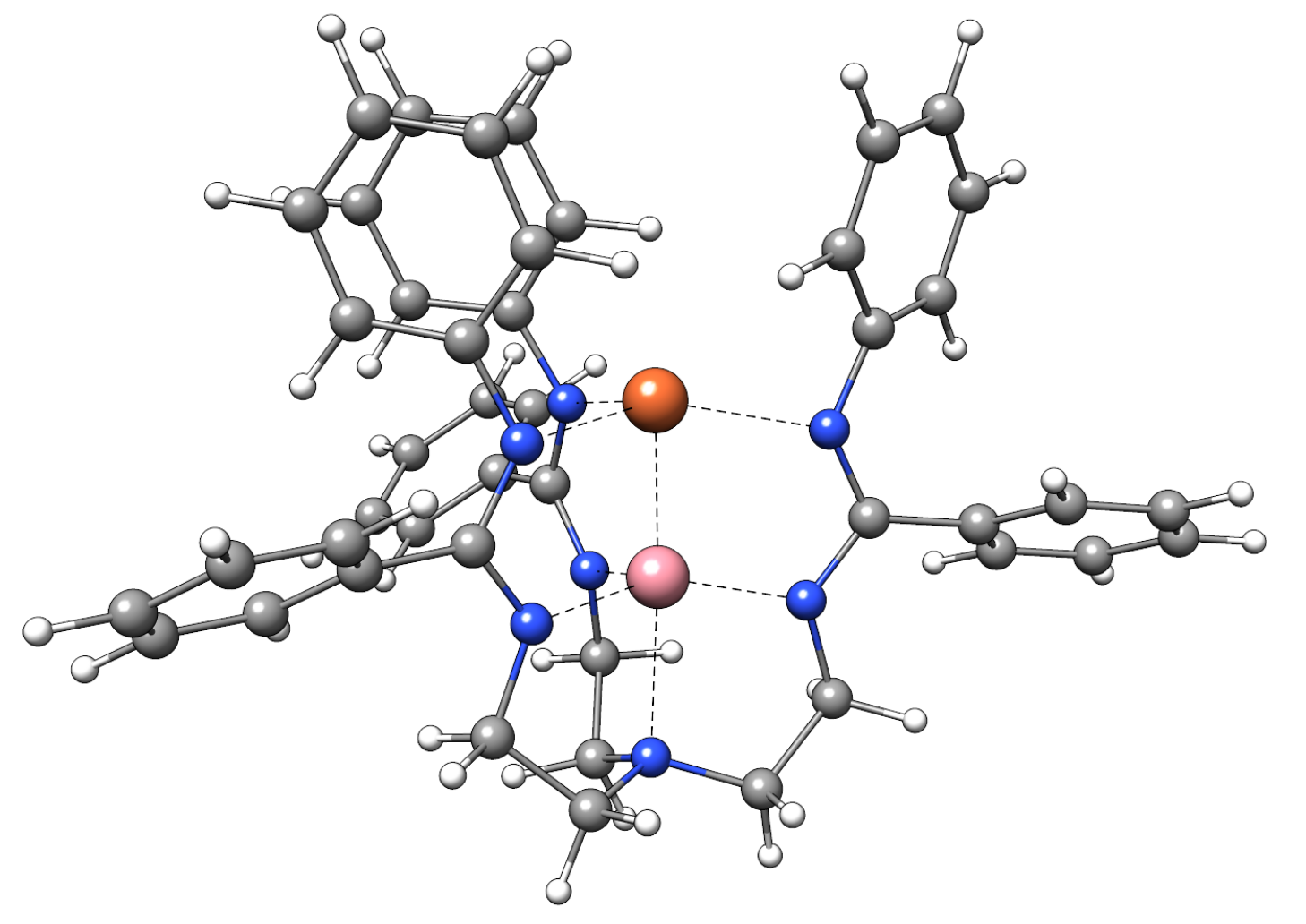
96
Co 4.2981 7.8875 -2.4539
Fe 4.2936 7.6860 -0.2490
N 4.3177 8.2394 -4.7611
N 2.5367 8.7591 -2.6654
N 2.3093 8.5146 -0.4585
C 2.8977 8.4151 -5.0518
H 2.4313 7.4287 -5.0575
H 2.7341 8.8807 -6.0379
C 2.1870 9.2538 -3.9732
H 2.4985 10.3023 -4.0724
H 1.1027 9.2137 -4.1534
C 1.8587 9.0585 -1.5831
C 0.5926 9.8363 -1.6028
C -0.5637 9.2492 -1.0959
H -0.5146 8.2451 -0.7007
C -1.7596 9.9421 -1.0971
H -2.6509 9.4763 -0.7029
C -1.8155 11.2325 -1.5975
H -2.7493 11.7751 -1.5960
C -0.6674 11.8282 -2.0926
H -0.7045 12.8389 -2.4730
C 0.5294 11.1352 -2.0985
H 1.4270 11.6140 -2.4622
C 1.9785 8.9213 0.8129
C 1.6789 10.2428 1.1731
H 1.6533 11.0098 0.4144
C 1.4548 10.5742 2.4929
H 1.2329 11.6001 2.7502
C 1.5192 9.6137 3.4891
H 1.3431 9.8845 4.5191
C 1.8213 8.3036 3.1506
H 1.8771 7.5470 3.9204
C 2.0494 7.9614 1.8355
H 2.2654 6.9364 1.5551
C 5.3288 9.1918 1.9786
H 5.5540 8.1404 1.7923
H 5.1441 8.9630 4.0893
N 5.5471 9.4758 -2.5880
N 5.4239 9.4980 -0.3630
C 5.1066 9.4430 -4.9974
H 4.4198 10.2884 -5.0609
H 5.6486 9.3764 -5.9534
C 6.1233 9.7533 -3.8739
H 7.0099 9.1183 -4.0024
H 6.4521 10.7963 -3.9819
C 5.8484 10.0894 -1.4741
C 6.6871 11.3166 -1.4253
C 6.2995 12.4761 -2.0920
H 5.3646 12.4913 -2.6351
C 7.0867 13.6116 -2.0320
H 6.7762 14.5093 -2.5474
C 8.2677 13.6012 -1.3084
H 8.8808 14.4891 -1.2624
C 8.6554 12.4529 -0.6380
H 9.5718 12.4449 -0.0664
C 7.8701 11.3159 -0.6942
H 8.1642 10.4190 -0.1694
C 5.2950 10.0694 0.8789
C 5.0337 11.4236 1.1229
H 4.9714 12.1140 0.2955
C 4.8255 11.8729 2.4115
H 4.6221 12.9211 2.5798
C 4.8647 10.9989 3.4848
H 4.6959 11.3605 4.4876
C 5.1147 9.6533 3.2589
N 5.5409 5.9316 -0.8551
C 6.9688 4.5777 -2.3437
N 5.5363 6.4511 -3.0183
H 6.1674 5.3706 -4.7257
H 6.9044 6.9670 -4.5066
C 4.8934 7.0165 -5.3047
C 5.9719 6.3998 -4.3893
C 6.0308 5.6968 -2.0668
H 4.0923 6.2814 -5.4031
H 5.3284 7.1836 -6.3039
C 6.0102 5.4138 0.3274
C 7.6940 4.5970 1.8539
C 5.0873 5.3600 1.3878
C 5.4599 4.9302 2.6424
C 6.7691 4.5391 2.8839
C 7.3321 5.0289 0.5932
H 8.0785 5.0923 -0.1832
H 8.7188 4.3056 2.0376
H 4.7300 4.8956 3.4388
H 7.0654 4.1993 3.8647
H 4.0598 5.6485 1.1710
C 6.5768 3.2760 -2.0424
C 8.6681 2.4371 -2.8654
C 8.2226 4.7949 -2.9076
H 7.1084 1.2072 -2.0670
H 5.6060 3.1067 -1.6000
C 9.0673 3.7296 -3.1624
C 7.4214 2.2136 -2.3040
H 8.5451 5.8037 -3.1213
H 10.0420 3.9086 -3.5932
H 9.3287 1.6068 -3.0670
> xtb mol.xyz --spinpol --tblite --uhf <UHF>
with <UHF> being the number of unparied electrons 0, 2, 4, 6, and 8 (with the correspond multiplicities 1, 3, 5, 7, and 9). The ground state is experimentally known to be a septet. The total energies in Hartree are shown below:
Multiplicity |
E(GFN2-xTB) |
E(spGFN2-xTB) |
|---|---|---|
1 |
-145.1025 |
-145.1025 |
3 |
-145.0996 |
-145.1185 |
5 |
-145.0870 |
-145.1712 |
7 |
-145.0574 |
-145.1904 |
9 |
-144.9653 |
-145.1209 |
and the spin-splittings with respect to the septet ground-state in kcal/mol are:
Multiplicity |
ΔE(GFN2-xTB) |
ΔE(spGFN2-xTB) |
|---|---|---|
1 |
-28.3 |
55.2 |
3 |
-26.4 |
45.2 |
5 |
-18.5 |
12.1 |
7 |
0.0 |
0.0 |
9 |
57.8 |
43.6 |
The correct gound state can be found with spGFN2-xTB but not with GFN2-xTB.
Please find more information on spGFNn-xTB methods in our publication:
H. Neugebauer, B. Bädorf, S. Ehlert, A. Hansen, S. Grimme, J. Comput. Chem., 2023, 44(27), 2120. DOI: 10.1002/jcc.27185