Introduction to CENSO

General information

Commandline Energetic SOrting (CENSO) is a sorting algorithm for efficient evaluation of Structure Ensembles (SE). The input ensemble (or single structure) originating from a CREST[SQM/FF] run can be ranked by free energy at DFT level and/or geometries can be optimized using DFT. CENSO has a modular structure, enabling efficient sorting at different levels of theory and targeting individual error sources, e.g., energy or solvation. Sorting is based on (free) energy windows or thresholds, within which all conformers/structures are considered. By choosing appropriate thresholds, the following “properties”/results can be obtained:

• lowest lying conformer and corresponding free energy

• fully optimized SE and averaged ensemble free energy

• Boltzmann populated SE at a given temperature

Apart from the refinement/sorting of SE, CENSO offers an automated approach to calculate NMR properties (shielding and coupling constants) or optical rotatory (OR) dispersion.

To perform fast calculations censo interfaces with QM codes like xtb, crest, TURBOMOLE and ORCA. The results are read by censo and evaluated in the sorting algorithm.

CENSO is the enhanced and more efficient successor of the ENSO program.

The main publication for the CENSO program can be found at J. Phys. Chem. A 2021.

Important

censo always keeps the conformer order of the input ensemble. E.g. CONF35 will correspond to the 35th conformer of the input ensemble.

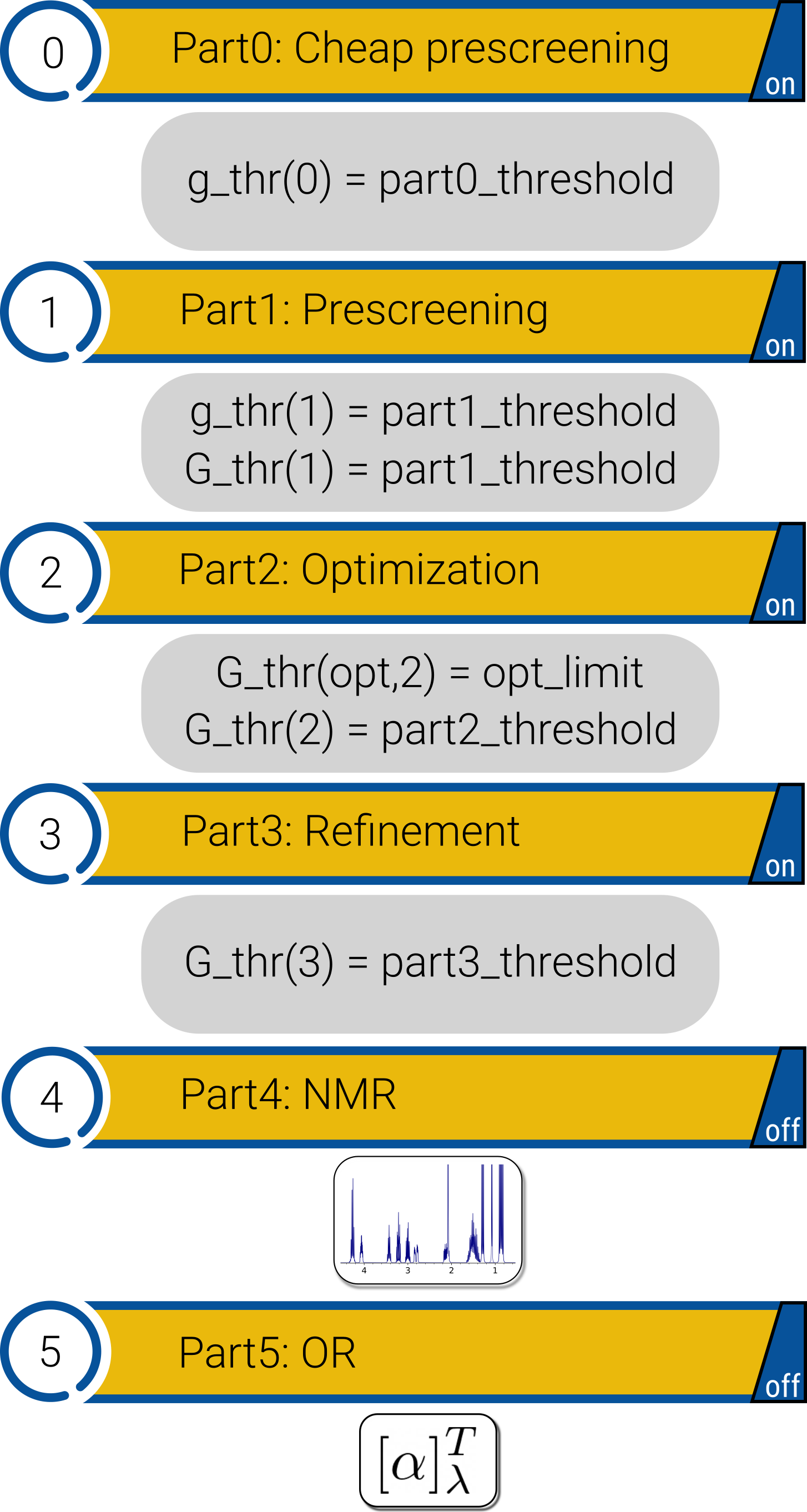
CENSO is structured into several parts, which can all be turned on or off by the user. These parts are presented in their intended order:

1. Part0: Cheap prescreening

2. Part1: Prescreening

3. Part2: Optimization (and free energy calculation)

4. Part3: Refinement (optional at higher hybrid-DFA level)

5. Part4: NMR-Mode

6. Part5: OR-Mode

Nomenclature: Free energies (G) are not available in each sorting step, due to the computational cost involved. Sorting-thresholds based on incomplete free energies e.g., without thermostatistical contribution (G_mRRRHO) are denoted by lower case g_thr and full free energies by upper case G_thr.

Parts 0-3 are concerned with efficient SE sorting, optimization and calculation of Boltzmann-weigths for populated structures. The parts are described in the following:

Part0 - Cheap prescreening:

Flexible and/or large molecules can have many conformers (i.e., several hundred) and sorting out truly high lying conformers fast is crucial for efficiency. This is the goal of part0. Here the electronic energy description is improved upon the initial SQM/FF energy by performing very fast B97-D3(0)/def2-SV(P)+gcp single-point calculations. If the molecule is in solution phase, solvation is treated at GFN2-xTB[ALPB] level. Sorting is based on g_thr(0) which has to be rather large, e.g. 4 kcal/mol or above.

Part1 - Prescreening:

Accurate electronic and solvation energies are calculated in part1. To be efficient COSMO-RS solvation contributions are calculated at r2SCAN-3c level, whereby both the gas phase electronic energy and solvation contribution is obtained and no additional calculations are necessary. Conformers above the threshold g_thr(1) are discarded. After sorting, thermostatistical contributions (G_mRRHO) are calculated at GFN2-xTB[ALPB] level using single-point hessian (Single Point Hessian (SPH) calculations) calculations. Full free energies are calculated and sorting is performed based on G_thr(1). The threshold can be automatically increased (fuzzy-threshold) as a function of the standard deviation of G_mRRHO, which is the case for flexible or diverse SE. Up to now all calculations have been performed on the SQM/FF input geometries!

Part2 - Optimization:

The relevant conformers/structures have to be optimized at DFT (r2SCAN-3c) level in implicit solvation (DCOSMO-RS). An efficient ensemble optimizer has been implemented, where all conformers are optimized for 8 iterations. Then a spearman correlation coefficient is calculated to check for parallel potential energy surfaces. If parallellity can be assumed, the sorting threshold G_thr(2) is decreased and conformers above the threshold are discarded, if their gradient norm is below a predefined threshold. For large ensembles, this decreases the number of high lying conformers fast. The batch wise optimization is repeated until all confomers within the energy window G_thr(2) are fully optimized. On the DFT optimized geometries free energies are calculated like in part1, with COSMO-RS(r2SCAN-3c) for E, dG_solv and GFN2-xTB[ALPB]-SPH for G_mRRHO. Boltzmann weights are calculated and an ensemble averaged free energy can be obtained. The conformers for use in parts 3-5 are considered up to a Boltzmann sum threshold, e.g., all conformers up to 90 % population are further considered.

Part3 - Refinement:

If it is necessary to refine the calculated Boltzmann weights at a higher (hybrid) DFT level, this can be performed in part3. Also it has to be noted, that Boltzmann weights calculated from rather accurate r2SCAN-3c energies are reliable enough for most applications. Like in part2 free energy contributions are calculated on DFT optimized geometries, although using a higher (hybrid) DFT level. Conformers below a Boltzmann sum threshold are considered further (e.g. in part4 or part5).

Optional property related parts (part4 and part5) are described below:

Part4 - NMR-Mode:

In part4 NMR properties can be calculated for the populated conformers. The Boltzmann weights are taken from either part1, part2 or part3 if they are available. All populated conformers up to the population part2_threshold or part3_threshold are considered. Coupling and shielding constants are calculated separately and can be calculated for the elements H, C, F, Si, P, or all elements. Files for further processing with ANMR are created. After the CENSO run, NMR spectra can be calculated using the ANMR code.

Part5 - OR-Mode:

In part5 optical rotatory (OR) dispersion of the populated structure ensemble can be calculated (TURBOMOLE only!). Boltzmann weights can be taken from part1, part2 or part3.